LCPG Principles
Fundamentals
Liquid crystal polarization gratings (PGs) are fascinating optical components that differ from traditional diffraction gratings, like ruled, Bragg, or holographic gratings. In particular, PGs exhibit polarization sensitivity, can have diffraction efficiency approaching 100%, and are much less sensitive to incident angle than, for example, Bragg or volume holographic gratings. To understand how this is possible, it is important to first understand how PGs work.
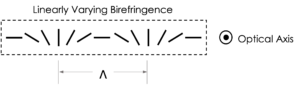
Instead of directly modulating the amplitude or phase of light, PGs periodically modulate the polarization states of light. This can be achieved by spatially varying the birefringence across the grating’s surface:
In the illustration above, the birefringence director can be seen to be smoothly rotating across the surface, transverse to the optical axis. When the director has rotated 180°, the director axis is again pointed in the starting orientation, defining the periodicity or grating pitch (Λ). In practice, this structure can be created by photoaligning and curing a liquid crystal polymer (i.e., reactive mesogen) to create a passive optical film with patterned birefringence.When the thickness of the birefringent PG layer provides a halfwave retardance for the incident light, circularly polarized illumination will change handedness, as it would with a homogenous half wave retarder. However, the phase of circularly polarized light is changed by 2θ when passing through a halfwave retarder that has been rotated by θ. This phase modulation occurs through geometric phase or Pancharatnam–Berry phase, which can occur when the optical wave is subjected to certain cyclic processes: in this case, the light changing from identical starting and ending polarization states via different paths.
Returning again to the illustration above, the continuous progression of the halfwave retarder axis presents a continuous phase progression for circularly polarized light. In this sense, the thin (< 10 μm) layer of the PG presents a smooth phase gradient like a thick glass wedge or prism, and the light is deflected efficiently in one direction. Because there are no discontinuities, the maximum theoretical diffraction efficiency for a PG is 100%, given analytically by
η_(±1)=(1∓S_3^’)/2 sin^2(πΔnd/λ). (1)
From Eq. 1, we see that η_(±1) is 100% when the light is circularly polarized (S’3 = ∓1) and the PG layer provides a halfwave of retardation (Δnd/λ = ½).
Meanwhile, the diffraction angle (θdiff) is described by the classic grating equation for first order diffraction
sin〖θ_diff 〗=λ/Λ+sin〖θ_inc 〗, (2)
where θinc is the incidence angle of the light. For the opposite handedness of circularly polarization, the phase gradient will have the opposite sign and the light will be steered to the opposite order. For light of mixed or linear polarization, the diffracted light will be decomposed into its orthogonal righthand and lefthand circularly polarized components.
Use in Non-Mechanical Beam Steering
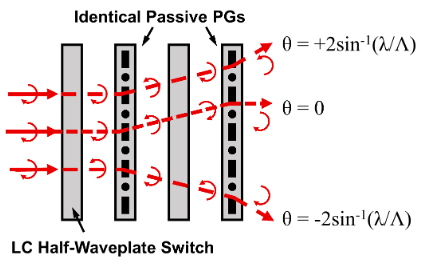
As shown above, PGs are thin transmissive elements that deflect light based on the polarization of incident light. Therefore, when a PG is preceded by a means of non-mechanically controlling the polarization state of light, it is possible to non-mechanically steer the incident light between the two ± 1 orders of the PG. This polarization control is easily achieved by liquid crystal variable retarders (LCVRs). Because both LCVRs and PGs are relatively thin, low-loss, transmissive components, it is feasible to optical bond several such non-mechanical beam steering subunits, or “stages,” together to increase the number of potential steering angles.
Non-mechanical beam steering provides many advantages over mechanical approaches such as motorized gimbals and prisms, particularly in their reduced size, weight, and power (SWaP) requirements. Among other non-mechanical and micro-mechanical beam steering technologies, such as optical phased arrays and microelectromechanical mechanical systems (MEMS) mirrors, PG beam steering assemblies are uniquely capable of steering both large angles and large apertures; Meadowlark Optics has demonstrated PG-based steering systems covering 120° field of regard and apertures up to 20 cm, making the technology useful for optical sensors and communications systems.
Unlike many steering technologies, non-mechanical beam steering with passive PGs is discrete, rather than continuous. The maximum number of steering angles (Nmax) available is dictated by the number of stages in the assembly (n), where Nmax = 2n. Therefore, a design optimization is required between the field of regard, angular resolution, and optical efficiency of the system. Please contact a Meadowlark Optics Solutions Engineer for assistance in specifying a custom PG beam steering system.
Liquid Crystal Polarization Lenses
Just as a linearly varying birefringence can be used to make a polarization-sensitive diffractive wedge (i.e., grating), a radially varying birefringence can be patterned to make a polarization-sensitive diffractive lens. Similar to the PGs, these polarization lenses (PLs) diffract incident light efficiently into a positive focal length for one handedness of circularly polarized light and into a negative focal length for the other handedness.
These PL components have several interesting properties. First, they are thin and lightweight alternatives to conventional refractive lenses. Second, they are highly chromatic, with chromatic dispersion opposite that of the material dispersion of common optical glasses.
When paired with LCVRs as in the PG beam steering architecture, PLs provide non-mechanical focus control. These non-mechanical refocusing systems have applications in microscopy, machine vision, and free-space optical systems.